Powtórka z Algorytmiki: Binary Search

Nigdy nie byłem orłem z algorytmiki. Wydaje mi się, że głównym powodem stanu rzeczy był brak faktycznego zastosowania. Na studiach miewałem zadanka jak np. logistyka, wyznaczanie optymalnej ścieżki pomiędzy punktami itd., jednak nic poza tym.

Oczywiście większość aplikacji musi przeszukać czy posortować dane, im optymalniej tym lepiej, jednak narzędzia do tego mamy albo gotowe (jak np. ElasticSearch) lub wbudowane w platformę (jak np. algorytmy sortowania). Powstaje więc pytanie: po co powinniśmy się uczyć algorytmiki?

Jakiś czas temu, dzięki warsztatom, w których uczestniczyłem, nabrałem nowego spojrzenia. Algorytmy rozwiązują archetypowe problemy w sposób bardzo generyczny, co pozwala nam na stworzenie oprogramowania, które będzie mniej wyspecjalizowane w obsłudze pewnych case-ów, co, teoretycznie, powinno poprawić reużywalność modułów, uprościć kod jak i logikę, która się za nim kryje.

Tak właśnie narodził się w mojej głowie pomysł stworzenia cyklu artykułów związany z algorytmiką. Być może tak samo jak i mi, komuś się przyda taka powtórka z Algorytmów i Struktur Danych.

Zacznijmy od jednego z najprostszych algorytmów: Binary Search.

Czym jest Binary Search?

Binary Search (pl: Wyszukiwanie Binarne) jest to algorytm opierający się na metodzie dziel i zwyciężaj. Wymaganiem do jego zastosowania jest posiadanie posortowanej tablicy.

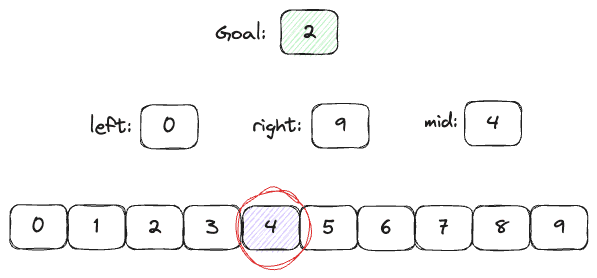
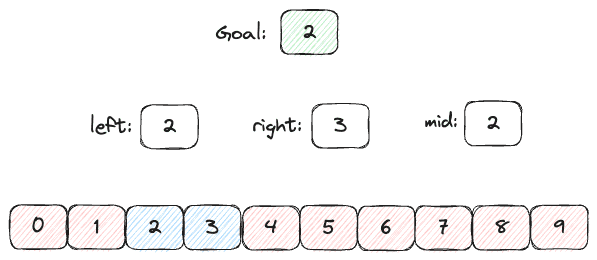
Aby jak najlepiej zaprezentować jak on działa na realnym przykładzie, załóżmy, że posiadamy tablicę dziesięciu numerów od 0-9.

Następnie musimy wyznaczyć nasz cel - element, który chcemy znaleźć. Niech to będzie cyfra "2". W następnym kroku musimy stworzyć dwie zmienne, które będą nam służyły za reprezentowanie zakresu tablicy jaki jeszcze pozostał do przeszukania: nazwijmy je left i right. Jako, że jest to algorytm oparty na metodzie dziel i zwyciężaj, musimy wybrać nasz punkt środa z wzoru:

$mid=\lfloor\frac{left + right}{2}\rfloor$ Co w naszym przypadku będzie wyglądało następująco:

$mid=\lfloor\frac{0+9}{2}\rfloor=\lfloor\frac{9}{2}\rfloor=\lfloor4.5\rfloor=4$

Wiemy, że będziemy sprawdzać piąty element naszej tablicy (4 to index, zaczynamy numerować od 0). Pod nim kryje się wartość 4, która jest większa od tej, której poszukujemy. Co pozwoli nam wyeliminować każdą następną wartość. Jednym sprawdzeniem wyeliminowaliśmy 60% danych!

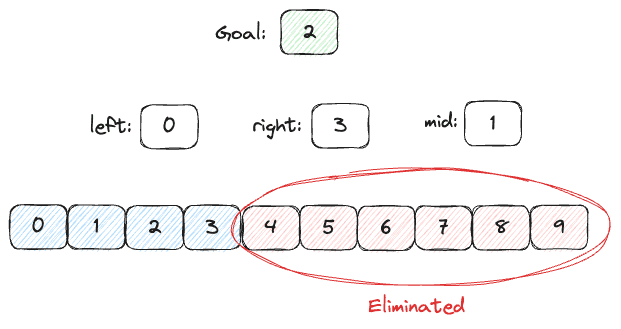
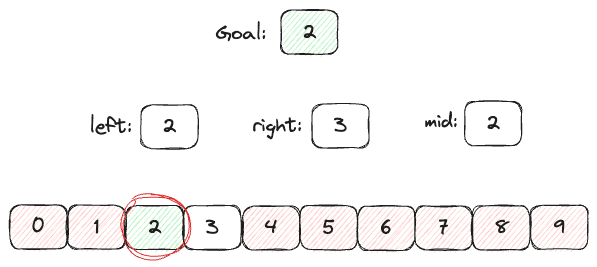
Dzięki temu możemy również zawęzić obszar naszych poszukiwań. Zmienną right możemy ustawić na wartość mid - 1, czyli wartość odpowiadającą elementowi przed ostatnio sprawdzanym. Oprócz tego ponownie będziemy musieli obliczyć nasz punkt środka, tym razem padł on na element o indeksie 1.

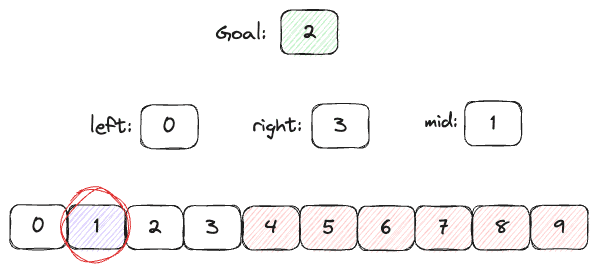
Wciąż nie dotarliśmy do naszej dwójki, jednak tym razem wartość, którą znaleźliśmy, okazała się mniejsza od poszukiwanej, czyli wszystkie elementy po lewej stronie odpadają nam do sprawdzenia. Naszą zmienną left możemy ustawić na wartość mid+1.

Wystarczy już tylko jeden obrót naszego algorytmu aby znaleźć nasz element!

To było proste i szybkie, co nie? 🙂 Musieliśmy sprawdzić tylko 3 elementy z naszej tablicy aby znaleźć ten, którego szukaliśmy.

Dzięki metodzie dziel i zwyciężaj algorytm jest w stanie znaleźć dowolny element (lub poinformować o braku takiego) w złożoności: $O(n)=\log_{2}n$ .

Implementacja

Jak wygląda jego implementacja w C#? Już spieszę z odpowiedzią. Zamiast zwykłej tablicy z numerkami spróbujmy wykorzystać strukturę danych. Załóżmy, że mamy listę studentów i musimy jak najszybciej odnaleźć dane studenta o pewnym Id.

Strukturę moglibyśmy reprezentować przy pomocy takiej klasy.

public class Student  
{  
    public int Id { get; set; }  
    public string Name { get; set; }  
    public int Age { get; set; }  
}

Do zdefiniowania naszego algorytmu będziemy potrzebowali funkcję, która przyjmuje dwa argumenty, Tablicę studentów jak i Id szukanego studenta.

Student? BinarySearchStudentById(Student[] students, int targetId)  
{  
 
}

Następnie będziemy musieli zdefiniować nasze zmienne left i right

static Student? BinarySearchStudentById(Student[] students, int targetId)  
{  
    int left = 0;  
    int right = students.Length - 1;  
}

Algorytm powinien działać tylko, dopóki te dwa wskaźniki nie spotkają się. Jeżeli doszło do takiego spotkania oznacza to, że szukanego elementu nie ma w naszej tablicy.

static Student? BinarySearchStudentById(Student[] students, int targetId)  
{  
    int left = 0;  
    int right = students.Length - 1;  
  
    while (left <= right)  
    {        
  
    }
    
    return null; // Student not found  
}

Kolejnym krokiem jest wyliczenie punktu środka:

static Student? BinarySearchStudentById(Student[] students, int targetId)  
{  
    int left = 0;  
    int right = students.Length - 1;  
  
    while (left <= right)  
    {        
	    int mid = left + (right - left) / 2;  
     
    }  
    return null; // Student not found  
}

Dzięki czemu możemy sprawdzić, czy element, który wyznaczyliśmy na środek jest tym, którego szukamy. Jeżeli nie, to w zależności czy jest wyższy czy niższy od szukanego elementu ustawiamy nową wartość jednego z wskaźników left lub right

Pisząc to trochę bardziej w formalnej notacji otrzymujemy:

\begin{cases} n=x, & \text{end algorithm} \\ n<x => left = mid + 1 \\ n>x => right = mid - 1 \end{cases}

Tak więc nasza końcowa implementacja będzie wyglądała następująco:

static Student? BinarySearchStudentById(Student[] students, int targetId)  
{  
    int left = 0;  
    int right = students.Length - 1;  
  
    while (left <= right)  
    {        
	    int mid = left + (right - left) / 2;  
  
        if (students[mid].Id == targetId)  
        {            
	        return students[mid];  
        }  
        if (students[mid].Id < targetId)  
        {            
	        left = mid + 1;  
        }        
        else  
        {  
            right = mid - 1;  
        }    
    }  
    return null; // Student not found  
}

Wydajność

Fajnie, że mamy działającą implementację. Zastanawiasz się jaki to może mieć wpływ na wydajność naszego rozwiązania?

Do zobrazowania jakości potrzebujemy przeciwnika dla wyszukiwania binarnego. Niech to będzie tzw. "Simple Search", czyli po prostu przejście po wszystkich elementach naszej tablicy i sprawdzenie czy znaleźliśmy naszą wartość

static Student? SimpleSearchStudentById(Student[] students, int targetId)  
{  
    foreach (var student in students)  
    {        
	    if (student.Id == targetId)  
        {            
	        return student;  
        }    
    }  
    return null; // Student not found  
}

Jako, że nie warto testować na jednym zbiorze danych, to przy pomocy biblioteki Bogus, stwórzmy generator studentów. Najważniejszym dla nas elementem będzie, aby mieli oni autoincrementowalne Id, dlatego też dla pola Id trzeba użyć propertisa: IndexFaker. Co więcej, jako że chciałbym, aby przy teście zawsze Id-ki zaczynały się od zera to stworzymy kilka instancji naszego generatora, tak aby każdy zbiór danych leciał od 0 do X.

public class BinarySearchBenchmark  
{
	// ...

	static Faker<Student> FakeStudentGenerator() => new Faker<Student>()  
	    .StrictMode(true)  
	    .RuleFor(x => x.Id, f => f.IndexFaker)  
	    .RuleFor(x => x.Age, f => f.Random.Int(18, 30))  
	    .RuleFor(x => x.Name, f => f.Name.FirstName());
}

A czym jest to nasze X? Przetestujmy wydajność na kilku zakresach tak, abyśmy mieli porównanie czy dla mniejszych zbiorów danych opłaca się stosować ten algorytm:

100
1 000
10 000
100 000
1 000 000

public class BinarySearchBenchmark  
{
	private readonly Student[] _100students = FakeStudentGenerator().Generate(100).ToArray();  
	private readonly Student[] _1000students = FakeStudentGenerator().Generate(1_000).ToArray();  
	private readonly Student[] _10000students = FakeStudentGenerator().Generate(10_000).ToArray();  
	private readonly Student[] _100000students = FakeStudentGenerator().Generate(100_000).ToArray();  
	private readonly Student[] _1000000students = FakeStudentGenerator().Generate(1_000_000).ToArray();  
	private Random _rnd = new Random();

   // ...
}

Do samego benchmarka użyjemy biblioteki BenchamrDotNet, jak ją setup-ować zapraszam do artykułu "BenchmarkDotNet - Jak sprawdzić szybkość naszego kodu". Nie mniej cały test będzie polegał na:

Wylosowaniu liczby z zakresu 0-X
Znalezieniu studenta o danych Id

public class BinarySearchBenchmark  
{
	[Benchmark]  
	public Student? SimpleSearch100()  
	{  
	    var targetId = _rnd.Next(0, 99);  
	    return SimpleSearchStudentById(_100students, targetId);  
	}  
	  
	[Benchmark]  
	public Student? BinarySearch100()  
	{  
	    var targetId = _rnd.Next(0, 99);  
	    return BinarySearchStudentById(_100students, targetId);  
	}
}

Nie będę wam wstawiał kodu do wszystkich zakresów,poradzicie sobie z implementacją.

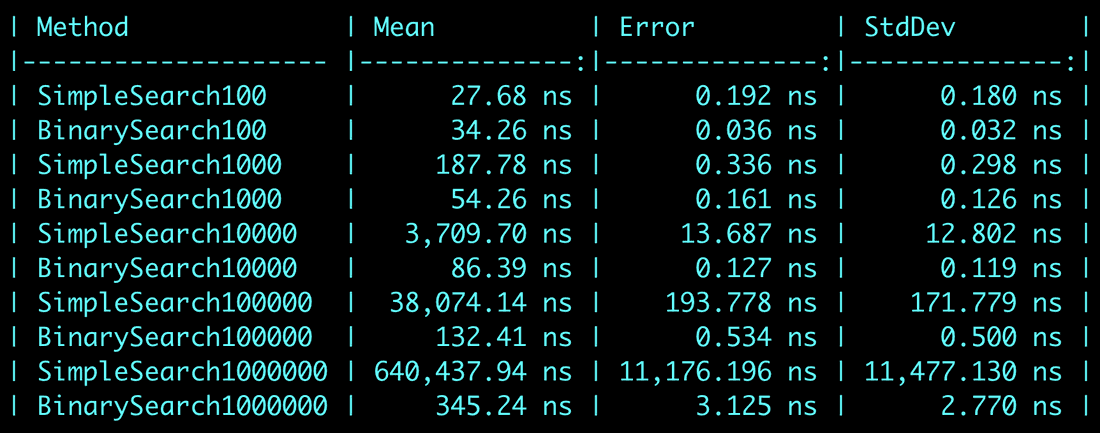
Jak wyglądają wyniki?

Ciężko o wielkie zaskoczenie. Dla niewielkiego zbioru danych jak np. 100 elementów simple search był szybszy (trzeba pamiętać że to było testowane na losowych danych, więc im mniejsze zbiory, tym większe znaczenie ma jakie zostały wylosowane elementy, dodatkowo trzeba pamiętać że w cache-u procesora zostanie załadowana cała linia a nie pojedyncza wartość), jednak nadal różnica pomiędzy simple search a binary search jest w takim wypadku minimalna.

Większe różnice pojawiają się już od 1 000 elementów. Tutaj widzimy że binary search był ponad 3-krotnie szybszy.

Przy kolejnych wartościach widzimy jak te dwa algorytmy się skalują, binary search nawet przy 1 000 000 elementów nadal działa bardzo szybko (ponieważ $\log_{2}1000000\approx20$ ). Natomiast SimpleSearch potrzebuje się napocić, aby znaleźć poszukiwany element.

Podsumowanie

Jak widzisz mój drogi czytelniku wyszukiwanie binarne może przynieść naprawdę duże oszczędności w czasie przetwarzania., a jest to naprawdę prosty algortym, który warto mieć w swoim toolbox-ie.

Mam nadzieje że artykuł się podobał!

Do Następnego 👋

Cześć!

Powtórka z Algorytmiki: Binary Search

Czym jest Binary Search?

Implementacja

Wydajność

Podsumowanie

Referencje

Dołącz do newsletter-a!